

Implementation of bubble sort in python def bubble_sort ( arr ): for i in range ( len ( arr ) - 1 ): swapped = False for j in range ( 0, len ( arr ) - i - 1 ): if arr > arr : arr, arr = arr, arr swapped = True if not swapped : return arr = bubble_sort ( arr ) print ( 'Sorted list: ', end = '' ) print ( arr ) Complexity Analysis Time Complexity of Bubble sort Pseudocode of Bubble Sort Algorithm bubbleSort( Arr, totat_elements) Thus, the sorted array will look like this: Thus marks the end of second pass where the second largest element in the array has occupied its correct position.Īfter the third pass, the third largest element will be at the third last position in the array.Īfter the ith pass, the ith largest element will be at the ith last position in the array.Īfter the nth pass, the nth largest element(smallest element) will be at nth last position(1st position) in the array, where ‘n’ is the size of the array.Īfter doing all the passes, we can easily see the array will be sorted. We now proceed with the third and fourth element i.e., Arr and Arr. So, no swapping happens and the array remains the same. We now proceed with the second and third element i.e., Arr and Arr. We proceed with the first and second element i.e., Arr and Arr. Thus, marks the end of the first pass, where the Largest element reaches its final(last) position. We proceed with the fourth and fifth element i.e., Arr and Arr. We proceed with the third and fourth element i.e., Arr and Arr. We proceed with the second and third element i.e., Arr and Arr. We need to sort this array using bubble sort algorithm.

This will continue until ith largest element is at the (n - i + 1) th position of the array.Ĭonsider the following array: Arr= 14, 33, 27, 35, 10. In real life, bubble sort can be visualised when people in a queue wanting to be standing in a height wise sorted manner swap their positions among themselves until everyone is standing based on increasing order of heights.Īlgorithm : We compare adjacent elements and see if their order is wrong (i.e a > a for 1 a, and a will always be greater than a when it is the largest element in range.When the list is already sorted (which is the best-case scenario), the complexity of bubble sort is only O(n). This is used to identify whether the list is already sorted.
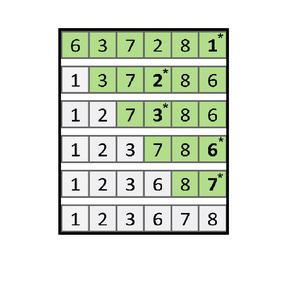
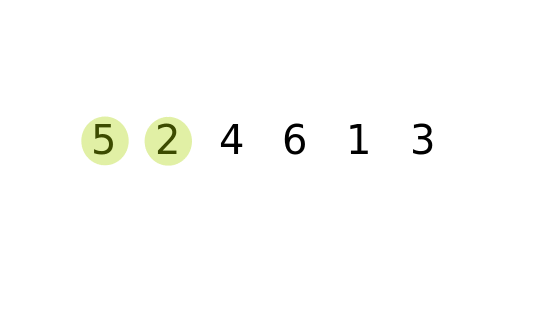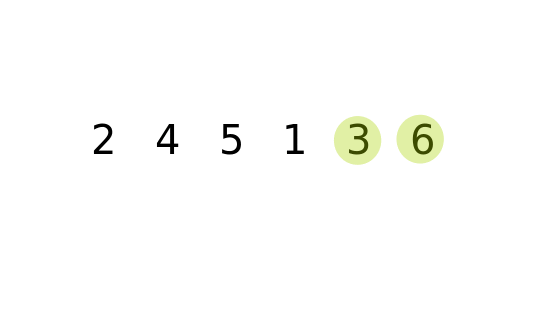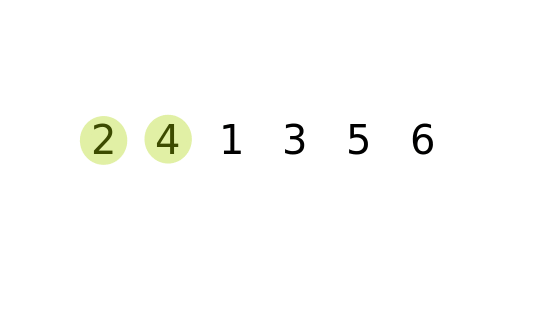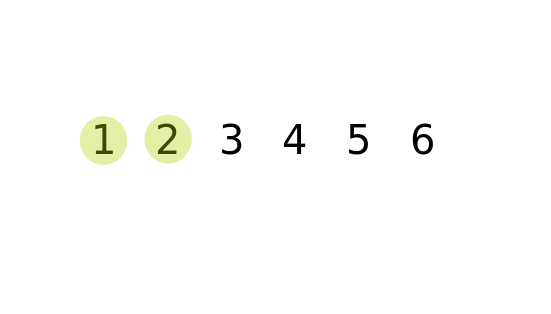
It is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in wrong order. the list of elements to be sorted is low. While selection sort must scan the remaining parts of the array when placing an element, insertion sort only scans as many elements as necessary.įurthermore, is bubble sort ever useful? Its a type of sorting, best used when the data is small. Simply so, which is better selection or insertion sort?įor small arrays (less than 20-30 elements), both insertion sort and selection sort are typically faster than the O(n*logn) alternatives. Selection sort is faster than Bubble sort. In selection sort, the sorted and unsorted array doesn't make any difference and consumes an order of n 2 (O(n 2)) in both best and worst case complexity. Selection sort has achieved slightly better performance and is efficient than bubble sort algorithm.


 0 kommentar(er)
0 kommentar(er)
